오늘은 머신러닝(Machine Learning)에 대해 공부했다.
머신러닝이란 무엇일까?
머신러닝 (Machine Learning)
- 컴퓨터를 인간처럼 학습시킴으로써 컴퓨터가 스스로 새로운 규칙을 생성하도록 하는 인공지능의 한 분야
- 컴퓨터가 학습이 가능하도록 할 수 있는 알고리즘과 기술을 개발한다.
- 사람이 명확하게 구분할 수 없거나, 많은 양의 지식들에 대한 규칙이 필요한 경우 사용된다.
알고리즘
- 수학, 컴퓨터 과학, 언어학 또는 관련 분야에서 문제 해결을 위해 정해진 절차나 방법을 공식화한 형태로 표현한 것
- 계산을 실행하기 위한 단계적인 절차
머신러닝에서 문제를 풀 때 회귀(Regression)와 분류(Classification)로 크게 나눌 수 있다.
머신러닝의 회귀와 분류
: 회귀 (Regression) :
- 출력 값이 연속적인 소수점으로 예측하게 하도록 푸는 방법
: 분류 (Classification) :
- 데이터를 클래스별로 구별하는 과정, 이진 분류(Binary Classification) 방법으로 나눌 수 있다. (0(Fail) 또는 1(Pass))
- 클래스가 여러 개로 나뉠 경우 다중 분류(Multi Label Classification) 방법을 사용한다.
다음은 머신러닝의 학습 유형 3가지이다.
: 지도 학습 (Supervised Learning) :
- 정답(입력값과 출력값)을 전부 알려주면서 학습시키는 방법
- 출력값이 존재하지 않으면 해당 방법으로 학습시킬 수 없다.

: 비지도 학습 (Unsupervised Learning) :
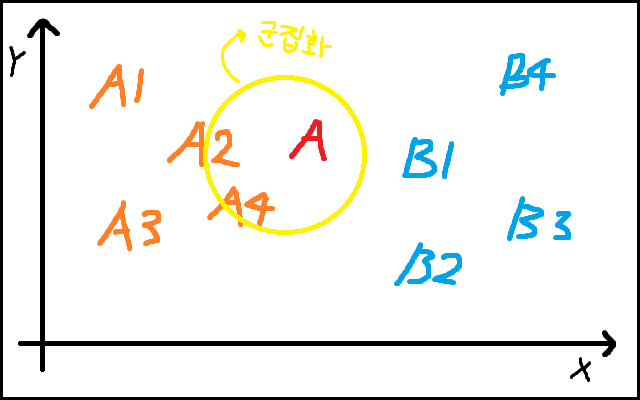
- 정답을 알지 못하는 상태에서 군집화(Clustering)하여 알아서 학습시키는 방법
- 출력값을 알지 못하는 상태일 때 효과적으로 사용이 가능하다.
- 비지도 학습의 종류
1. 군집(Clustering)
2. 시각화(Visualization)와 차원 축소(Dimensionality Reduction)
3. 연관 규칙 학습(Association Rule Learning)

: 강화 학습 (Reinforcement Learning) :
- 주어진 데이터가 없는 상태로 실행과 오류를 반복하면서 학습하는 방법
- 대표적으로 알파고와 같은 것이 있고, 게임과 같은 곳에서 주로 사용한다.
- 강화 학습의 개념
1. 에이전트(Agent)
2. 환경(Environment)
3. 상태 (State)
4. 행동 (Action)
5. 보상 (Reward)

다음으로는 머신러닝에서 사용하는 것 중 하나인 선형 회귀(Linear Regression)에 대해서 알아보자.
선형 회귀 (Linear Regression)
- 임의의 직선(가설)과 점(정답)의 거리, 가설(Hypothesis)과 손실 함수(Cost or Loss Function)
- 알고리즘이 예측하는 값의 최적화(Optimization)를 위해 손실 함수를 최소 할수록 좋다.
- x와 y의 관계를 나타내는 직선이 존재하고, 변수 사이의 선형 관계를 모델링한 것
- 입력값(x)이 2개 이상으로 존재한다면 다중 선형 회귀(Multi-Variable Linear Regression)를 사용한다.
- 다중 선형 회귀 : 선형 회귀와 똑같지만 입력 변수가 여러 개인 경우를 말한다.
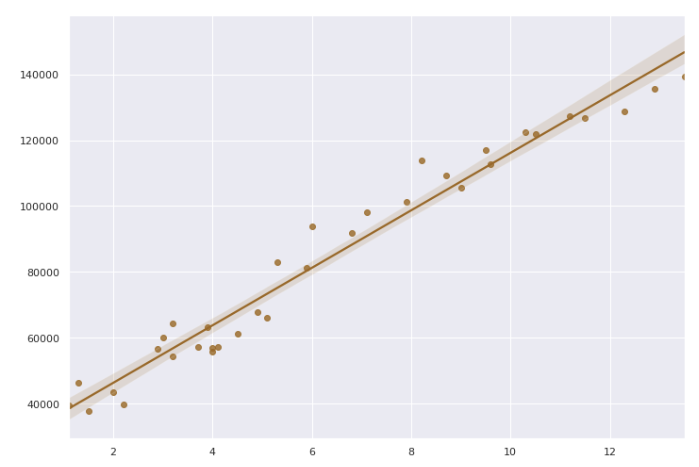
만약, 선형 회귀로 표현할 수 없는 곡선(U자)의 형태를 지닌 그래프가 있다고 생각해보자.
해당 그래프는 선형 회귀로 표현하기에는 어려움이 있기에 손실 함수를 최소화(Optimize)할 수 있는 경사 하강법(Gradient Descent Method)이라는 방법을 사용한다.
경사 하강법 (Gradient Descent Method)
- 함수의 경사(Gradient)에서 Cost의 손실 함수를 최소화하는 방법
- 컴퓨터가 임의의 초기값을 잡고 점진적으로 문제를 해결하는 방법
- 기울기가 낮은 쪽으로 한 칸씩 전진하며 Minimum에 이르도록 반복한다, 이때 한 칸씩 전진하는 단위를 Learning rate라고 한다.
- Learning rate가 작다면 많은 시간이 소요되고, 크다면 계속 진동하다가 발산하게 되는 Overshooting이 일어날 수 있다.
- 경사 하강법의 목표는 시작 지점으로부터 가까운 Local Cost Minimum를 찾는 것이 아니라 손실 함수의 가장 최소점인 Global Cost Minimum을 찾는 것이다.


머신러닝 모델이 만들어진다면 학습하고 검증하고 테스트를 거쳐야 하는데, 해당 부분의 데이터를 맡는 3가지 데이터셋이 존재한다.
데이터셋 분할
1. 학습 데이터셋 (Training set) : 예시 : 교과서
- 머신러닝 모델을 학습시키기 위해 사용한다.
- 전체 데이터셋 중 가장 많은 비율을 차지한다.
2. 검증 데이터셋 (Validation set) : 예시 : 모의고사
- 머신러닝 모델의 성능을 검증 및 튜닝하는 용도로 사용한다.
- 정답 라벨이 있으며 학습 단계에서 사용하지만, 모델에게 데이터를 직접 보여주진 않는다.
- 손실 함수 및 Optimizer 등을 바꾸면서 모델을 검증한다.
3. 평가 데이터셋 (Test set) : 예시 : 수능
- 정답 라벨이 없는 실제 환경에서의 평가를 위해 사용한다.
앞서 알아본 선형 회귀의 방법은 실제 자연 및 사회현상에 있는 특정 변수들에 대해 대처하기 힘들다.
보통 이러한 현상에 대해서는 선형이 아닌 S 커브의 형태를 따르는 경우가 많은데, 이때 사용하는 것이 논리 회귀(Logistic Regression)이다.
논리 회귀 (Logistic Regression)
- 0(Fail)과 1(Pass)의 선택지에서 하나를 결정하는 이진 분류(Binary Classification) 문제를 다루는 알고리즘이다.
- 선형 회귀로 나타내기 힘든 형태를 논리 함수(Logistic Function)를 사용하여 나타낸다.
- 일부 특정 변수에 대한 확률 값이 선형이 아닌 S 커브의 형태를 띨 때, 해당 S 커브를 함수로 표현한 것이 논리 함수(Logistic Function)라고 부른다.
- 딥러닝에서는 시그모이드 함수(Sigmoid Function)라고 부르지만, 같은 맥락이다. (Logistic Function = Sigmoid Function)
- 실질적인 계산은 선형 회귀와 똑같은 형태를 띠고 있지만, 출력에 Sigmoid Function을 붙여 0과 1 사이의 값을 가지도록 한다.

논리 회귀도 선형 회귀와 마찬가지로 손실 함수를 최소화하는 방향으로 가야 한다.
하지만 논리 회귀는 0과 1의 값으로 나와야 하기 때문에 확률분포표 상에서 정답 값이 0이면 0에, 1이면 1에 가깝게 나와야 한다.

해당 논리 회귀에서 확률 분포의 차이를 최소화하여 가장 정답 값에 근사한 그래프처럼 만들어주기 위해서는 CrossEntropy라는 함수를 사용한다.
위에서 선형 회귀와 논리 회귀에 대해서 얘기했다.
둘 다 공통적이게 손실 함수라는 단어를 언급했는데, 손실 함수는 대체 무엇일까?
손실 함수
- 주로 통계학, 경제학 등에서 많이 쓰이는 함수이다.
- 머신러닝에서의 손실 함수는 예측값과 실제값에 대한 오차를 줄이는 데 유용하게 사용된다.
다음은 논리 회귀에서 다수의 클래스로 구분하는 문제를 다룰 때는 다항 논리 회귀(Multinomial Logistic Regression)를 사용한다.
다항 논리 회귀를 사용하여 다항 분류 문제를 풀 때 원핫 인코딩(One-hot Encoding)과 Softmax 함수를 사용한다.
원핫 인코딩(One-hot Encoding)
- 컴퓨터가 이해하기 쉽게 입력을 하여 확률 분포 그래프를 그려주는 방법
- 여러 개의 항을 0과 1로 표현해줄 수 있다.
: One-hot Encoding을 만드는 방법 :
1. 클래스 수만큼 배열을 0으로 채운다.
2. 각 클래스의 인덱스 위치를 정해준다.
3. 각 클래스에 해당되는 인덱스 위치에 1을 넣는다.
Softmax Function
- 선형 모델에서 나온 결과를 모두가 더하면 1이 되도록 만들어주는 함수
- 여러 가지 다른 결과에 비슷한 가중치를 준 뒤 모두 더했을 때 1이 되도록 만들어준다.
그렇다고 해서 확률 분포의 차이를 계산할 때 CrossEntropy 함수를 쓰지 않는 것은 아니다.
항이 여러 개가 되었을 뿐 이진 논리 회귀와는 별 차이가 없기 때문이다.
다음으로는 다양한 머신러닝 모델과 분류기에 대해서 알아보자.
분류기 (Classifier)
- 각 다른 객체 A와 B에 대해 구분하는 문제를 분류 문제(Classification Problem)라고 하고, 해당 분류 문제를 푸는 모델을 분류기라고 한다.
- 서로 다른 객체를 분류할 때 객체 사이의 분류된 선을 기준으로 나눈다.
다양한 머신러닝 모델
: SVM (Support Vector Machine) :
- 분류된 선을 기준으로 객체 간의 거리가 최대가 되는 점을 Support Vector, 가장 가까운 객체들의 거리를 Margin이라고 한다.
- Margin이 클수록 Classifier의 성능이 좋다.
- 만약 특성(Feature)이 다른 예외의 상황이 발생하면 구분하기 힘든 상황이 나올 수 있다.
: KNN (K-Nearest Neighbors) :
- 비슷한 특성을 가진 개체끼리 군집화해주는 알고리즘이다.
: Decision Tree (의사결정 트리) :
- 스무고개와 비슷한 방식으로, 성능이 괜찮아서 간단한 문제를 풀 때 자주 사용한다.
: Random forest :
- Decision Tree를 여러 개로 합친 모델이다.
- 각 Decision Tree의 결과를 모아서 투표(Majority Voting)를 통해서 최종 결과값을 결정하는 것이다.


마지막으로 머신러닝에서 가장 많은 비율을 차지하며, 중요한 작업인 전처리(Preprocessing)에 대해 알아보자.
전처리 (Preprocessing)
- 머신러닝에서 가장 많은 비율을 차지하는 중요한 작업
- 넓은 범위의 데이터 정체 작업이다.
- 필요 없는 데이터를 지우고 필요한 데이터만 취하거나, Null 값이 있는 행을 삭제한다.
- 전처리 작업을 하게 되면 학습 속도가 빨라지고, Local Minima에 빠질 가능성을 줄여준다.
- 머신러닝에서 전처리 작업을 하지 않으면 성능이 저하되거나 학습이 되지 않는 등의 악영향이 생길 수 있다.
- 정규화(Normalization) 및 표준화(Standardzation) 등의 많은 작업을 내포하고 있다.
: 정규화(Normalization) : 데이터를 0과 1 사이의 범위를 가지도록 만든다, 같은 특성인 데이터 중에서 가장 작은 값을 0, 가장 큰 값을 1로 만들어준다.
: 표준화(Standardzation) : 데이터의 분포도를 정규 분포의 형태로 바꿔준다, 데이터의 평균이 0이 되도록 하고, 표준 편차가 1이 되도록 만들어준다.
-
어제오늘 머신러닝에 대해 공부했다.
아무래도 처음 접하는 분야이기에 이해하는데 많은 시간이 소요됐다..
아직까지도 이해가 잘 되지 않는 부분이 많이 있기 때문에 배운 걸 다시 보고.. 다시 보고.. 계속 반복했다.
그래도 개념에 대해 공부하기도 하고, Colab을 이용해서 실습도 해보니까 이해가 조금씩 됐다.
왠지 머신러닝은 계속 복습해가면서 기억해야 될 것 같다.
:D
'TIL 및 WIL > TIL (Today I Learned)' 카테고리의 다른 글
| [TIL] 2022.05.17 (Machine Learning, 머신러닝3) (1) | 2022.05.17 |
|---|---|
| [TIL] 2022.05.16 (Machine Learning, 머신러닝2) (0) | 2022.05.17 |
| [TIL] 2022.05.12 (Git-Github, 머신러닝0) (0) | 2022.05.12 |
| [TIL] 2022.05.11 (인스타 UI 클론 코딩 - 팀 프로젝트(끝)) (0) | 2022.05.11 |
| [TIL] 2022.05.10 (인스타 UI 클론 코딩 - 팀 프로젝트4) (0) | 2022.05.11 |



